Retinal Oxygen Transport: Physics-Informed Modeling

1. Classical Numerical Methods

• Finite Difference Method (FDM) with adaptive time-stepping
• Finite Volume Method (FVM) ensuring exact mass conservation
• Validated against analytical solutions with < 0.1 % error

2. AI-Powered Physics-Informed Neural Networks

• Inverse PINNs for discovering diffusivity and reaction rates from sparse/noisy measurements
• Transformer-based architecture with multi-head attention for enhanced spatial learning
• Forward PINNs for direct PDE resolution (coming soon)

3. Comprehensive Validation Framework

• Cross-method comparisons to demonstrate consistency and robustness
• Integration pipeline for experimental and synthetic datasets
• Clinical relevance assessment against published physiological measurements

FVM

It subdivides the domain into control volumes and enforces exact conservation of mass by integrating fluxes across each cell's faces, typically with backward-Euler discretization for stability. FVM provides our benchmark steady-state solution. We validate its outputs against the analytical steady-state profile and against COMSOL's stationary study. These results serve as the reference for assessing the accuracy of our inverse PINN and forward PINN.

FDM

A discretizes the reaction–diffusion equation on a uniform spatial grid, using difference formulas for second derivatives and explicit (or implicit) time-stepping schemes. We employ FDM to simulate the full time-dependent evolution of oxygen concentration across all four retinal layers. This lets us quantify the characteristic stabilization time (τ) and generate transient profiles that we compare directly against COMSOL time-dependent runs and our PINN Forward Model.

PINN Reconstruction of Oxygen Profile

A neural collocation approach where a network is trained to satisfy the governing PDE and boundary conditions throughout the domain, producing a continuous function approximation of C(z,t). This model offers a purely data-driven solver for both transient and steady-state problems—no grid required. Once integrated, it will be directly compared to our FDM/FVM benchmarks for speed, accuracy, and mesh-independence.

This neural network consists of 6 layers with 256 neurons each, and a tanh activation function. It is trained with an adaptive loss weighting to balance the PDE, boundary, and data constraints. The training loss is calculated as the sum of the PDE, boundary, and data losses. The PDE loss is calculated as the mean squared error of the PDE residual, the boundary loss is calculated as the mean squared error of the boundary conditions, and the data loss is calculated as the mean squared error of the data. The training loss is then used to update the weights of the network. The network is trained for 10000 iterations, and the best model is saved.

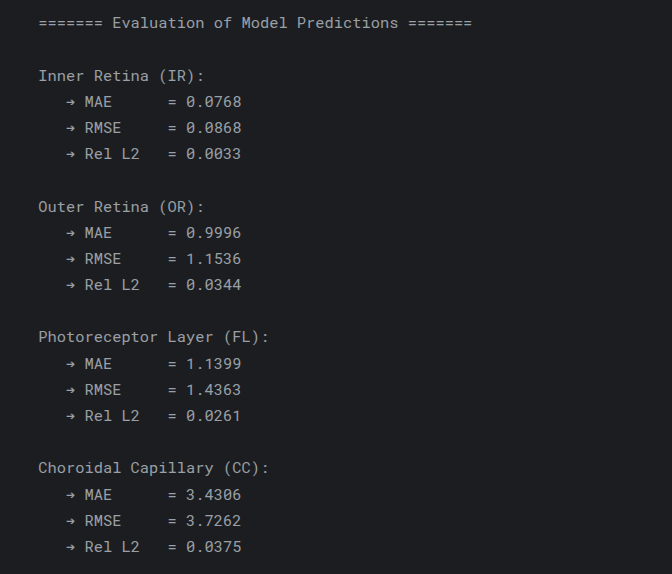
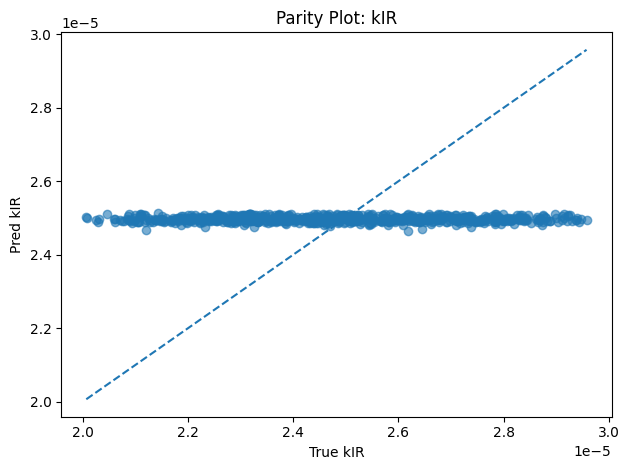
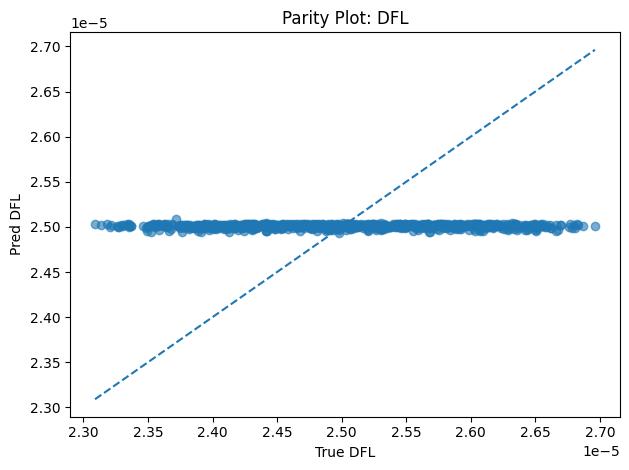
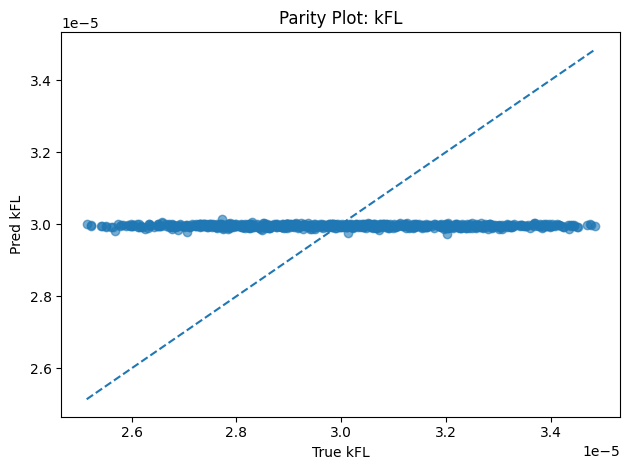
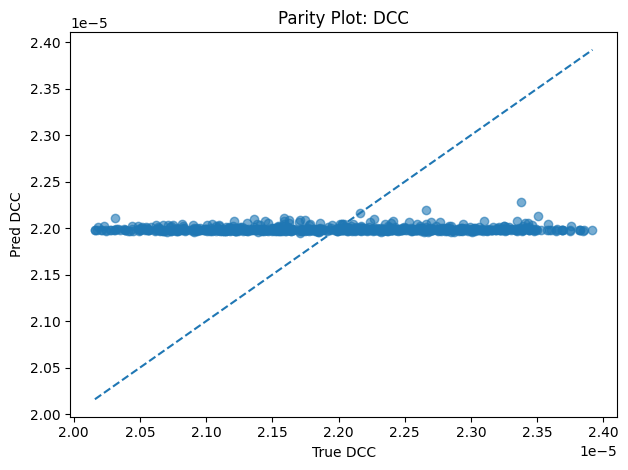
Inverse PINN Parameter Recovery

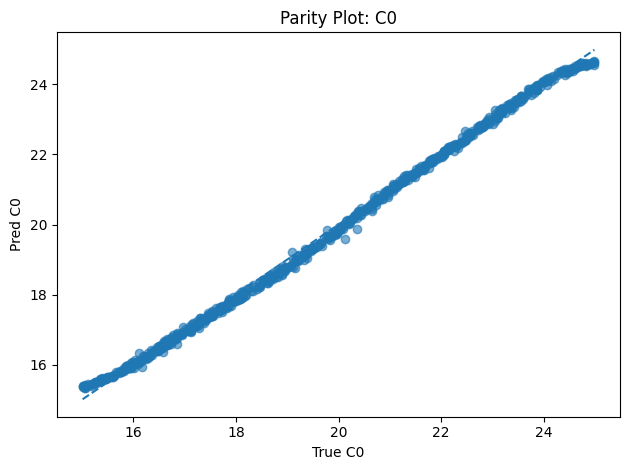
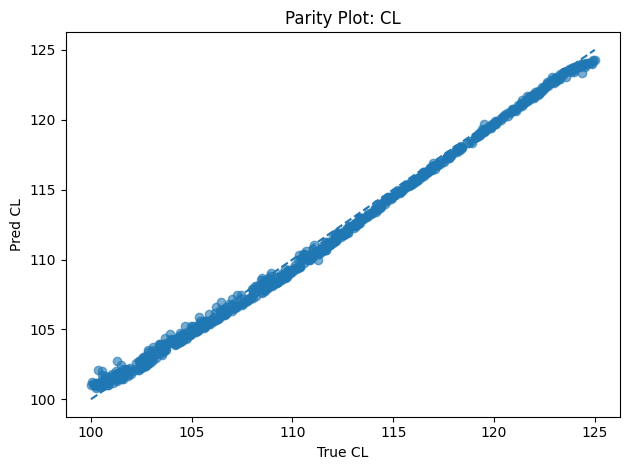
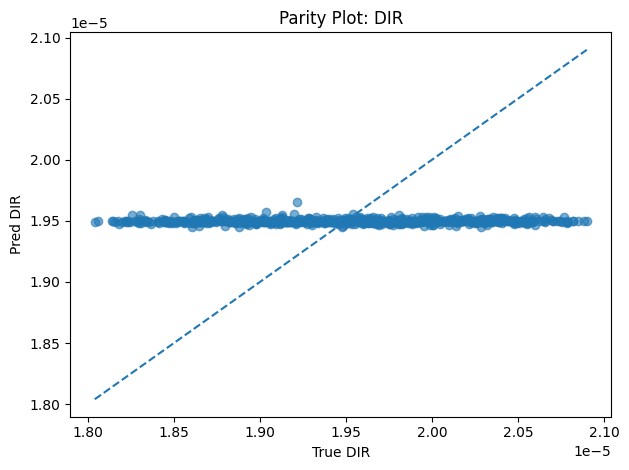
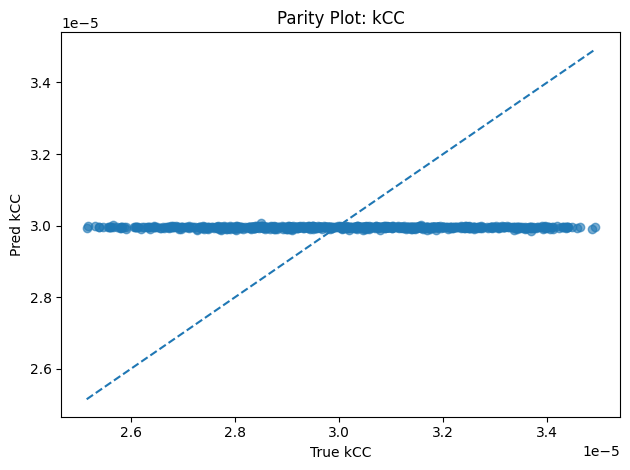
A neural network that infers unknown physical parameters (e.g. layer diffusivities 𝐷𝑖, reaction rates 𝑘𝑖, boundary concentrations) by minimizing a composite loss: PDE residuals + interface continuity + boundary enforcement + data mismatch. We train this model on synthetic profiles (with added noise) to recover ground-truth parameters with > 95 % accuracy and R2>0.99. Its outputs are then validated and used to demonstrate robust parameter estimation from sparse measurements.

COMSOL

To independently verify our in‑house finite‑difference and finite‑volume solvers, we implemented the same four‑layer retinal O₂ transport model in COMSOL 6.1. Using its Coefficient Form PDE interface, we represented each 200 µm segment (inner retina, outer retina, fluid, choroid) with the same diffusivity and metabolic rates as our code, applied physical boundary pressures at the ends, and ran a time‑dependent study from 0 to 30 s. COMSOL’s built‑in handling of layer interfaces ensured smooth continuity of both concentration and flux. The resulting transient curves and steady‑state gradient matched our numerical results exactly, providing an independent validation of our methodology.

1. Diabetic Retinopathy

• Simulate hypoxia-induced tissue damage
• Predict progression and optimize intervention timing

2. Age-Related Macular Degeneration

• Quantify choroidal circulation deficits
• Guide treatment strategies

3. Retinal Vein Occlusion

• Map localized hypoxic zones
• Aid surgical decision-making

Physics-Informed Multi-Loss Architecture

$$\text{Total Loss} = \lambda_{\text{PDE}} L_{\text{PDE}} + \lambda_{\text{B}} L_{\text{Boundary}} + \lambda_{\text{C}} L_{\text{Continuity}} + \lambda_{\text{D}} L_{\text{Data}}$$

• L_PDE: Enforces the reaction–diffusion equation
• L_Boundary: Applies physiological boundary conditions
• L_Continuity: Ensures flux continuity across layers
• L_Data: Matches experimental measurements

Transformer-Enhanced PINN

• Captures inter-layer spatial dependencies
• Pre-training on synthetic datasets accelerates convergence
• Physics-informed fine-tuning preserves biophysical realism